试想有一列高速运动的火车，火车的中间有一个随时可以亮起的光源，火车的中央和站台分别有一位观察者。当火车经过站台的时候，车内的光源向两边发射出两道光线，那么他们观察到的情况会是相同的吗？

对于火车上的人来说，他相对于火车静止，因此两束光线同时到达车头和车尾。但对于站台上的人来说，由于光速恒定且火车向前行驶，光线到达车头的距离大于到达车尾的距离，所以在站台上的人看来，光线是先到达车尾再到达车头。

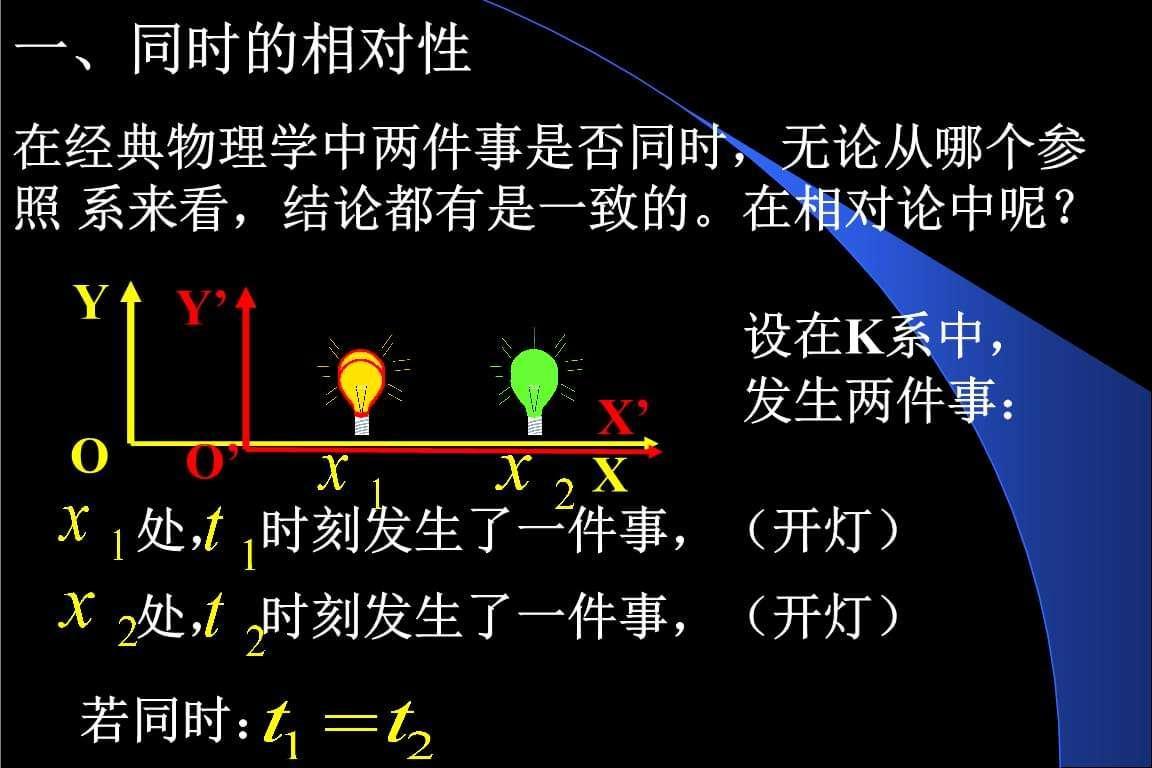
也就是说在火车上发生的同一件事情，对于火车上的人来说是同时发生的，但在车外的人看来是有先后顺序的，这就是狭义相对论的同时相对性，即在一个参考系中同时发生的两件事，在另一个参考系看来不是同时发生的或者说同时也是相对的。

根据狭义相对论，物体在运动方向上的长度会被压缩，即尺缩效应，而这种效应会产生一个悖论，一列高速运动的火车，经过一个与火车长度相同的隧道时，火车和隧道的长度还是相同的吗？

要解答这个问题，我们需要考虑火车司机和隧道管理员两种角色观察到的情况。当火车高速驶入隧道时，在火车司机的参考系看来火车是静止的，而隧道则是向着火车高速运动而来，隧道的长度应该收缩变短。但从隧道管理员的参考系来看，隧道是静止的，火车是高速运动的，火车的长度应该收缩变短。

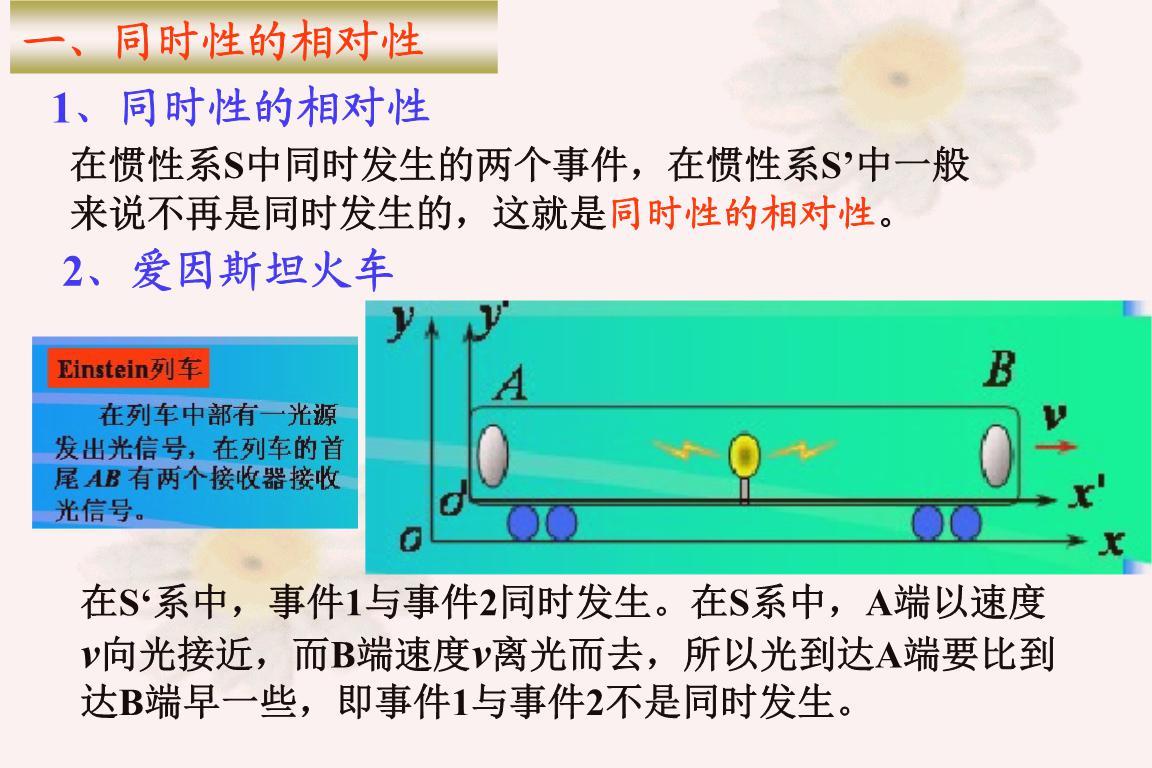
综上所述，隧道管理员的观点是火车的长度更短，而火车司机的观点是隧道的长度更短。为了验证自己的观点，火车司机和隧道管理员分别设计了一个实验。隧道管理员的实验是在隧道两头放置两个闸门A和B，当火车完全进入隧道后，把隧道前后的闸门关一下再瞬间打开。由于他的观点是火车比隧道短，所以闸门不会出触碰到火车。

火车司机的实验是在火车两头装有烟花，当火车车头刚出隧道时，火车两头同时发射烟花。由于他的观点是隧道的长度更短，所以烟花都应该会发射到隧道外，结果是他们的实验都成功了，但这两个实验的结论是相互矛盾的。

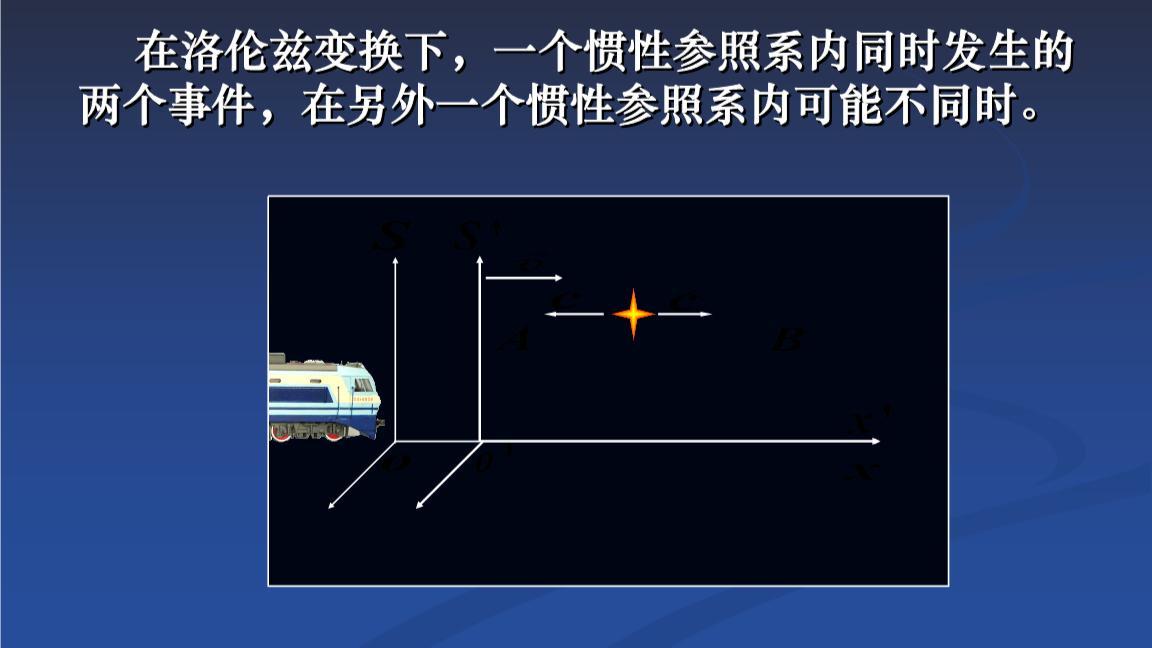
事实上，这两个实验在理论上都是可以成功的，不过都是在各自参考系下的成功。比如隧道管理员的实验，在他看来自己同时关闭了闸门A和B，但由于同时的相对性，在火车司机看来，隧道管理员并没有同时关闭两个闸门。

因为在他眼中隧道是向左高速运动的，所以他觉得隧道前方的闸门B先关闭，此时的火车还没有完全进入隧道，等火车完全进入隧道后，隧道后方的闸门A才关闭。因为闸门只关闭了一瞬间，所以先关闭的闸门B已经打开了，因此火车可以顺利通过。

这个实验结果就证明不了火车更短，同样对于火车司机的实验在火车司机看来，自己是同时发射了烟花C和D，但由于同时的相对性，在隧道管理员看来，火车司机并没有同时发射烟花C和D。在他眼中火车是向右高速运动的，因此他觉得后方的烟花C先发射，然后火车继续向前行驶了一段时间后，前方的烟花D才发射，因此这个实验也证明不了隧道更短。

综上所述，我们只能得出这样的结论，绝对的同时性并不存在，也不存在一个特定的参考系，使得我们可以宣布在这个参考系里这两件事情完全同时发生。但所有这些参考系下得到的这些结果都是准确有效的。因此真正的绝对时间是不存在的，我们各自感知的事件并不相同，时间是相对的。

最后我们再来考虑一个问题，从狭义相对论的这两个方程来看，当物体运动的速度越大，其在运动方向上的长度越小，物体的质量越大。但是当运动速度趋近于光速时，物体的质量将变得无限大，长度将趋近于零。

因此狭义相对论认为，任何物体的运动速度不能超过光速，但是我们从另一个方面去思考，如果物体的运动速度超过了光速，右侧的根号里将会变为一个负数，而将负数开根号就会得到一个虚数。

因此从这个意义上来说，如果虚数存在物理意义，在狭义相对论中虚数的物理意义就是超光速。